机器学习

基础或专业术语

数据集(Training Set)

用于训练模型的数据集合，一般具有输入特征（x = "input" variable feature）输出特征（y = "output" variable or "target" variable）序号（m = number of training examples）。输入输出构成一条训练数据（x，y） = single training examples。（x，y）之上可以加上^(i)，用于表示这是第几个训练数据：比如

$$(x^{(i)},y^{(i)}) = i^{th} \text{\,\,training example}$$

输入输出和函数

机器学习中函数（Model）一般用f表示，输入（feature）常为x，真实输出为y，我们预测的输出（prediction）为$\hat{y}$（表示输入x通过函数的预测输出值）

如何计算模型f

我们以线性模型举例：$f_{w,b}(x) = wx + b$ 我们要求模型f，实际就是要求w和b（即模型参数或者权重）的值。w和b一般就是基于x和$\hat{y}$来求得。

代价函数公式（cost function也可以叫成本函数）

$\hat{y} = f_{w,b}(x^{(i)})$或者$f_{w,b} = wx^{(i)}+b$
所以我们要找到w,b满足：$\text{对于所有的}(x^{(i)},y^{(i)})\text{都有}\hat{y}接近y^{(i)}$
代价函数就是来计算当前预测值$\hat{y}$和真实值y之间的差异.
常用的是平方误差代价函数：$$J(w,b) = \frac{1}{2m}\sum_{i = 1}^m(y - \hat{y})^2$$
或者$$J(w, b) = \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})2$$
这里使用2m是为了让计算更简洁，后续求权重偏导的过程中会出现一个2，在这里正好可以约去。
我们求模型的目标也就是让这个J尽可能地合理地小一些.
所以不同的权重比如w,b会有不同的J，J值与权重的映射又组成了一个函数，我们需要在这个函数中寻找J最小值所对应的权重。

可视化代价函数

可以建立一个3D图，或者使用等高线来表示。

梯度下降（gradient decent）

所以我们要找到合适的权重就是要找到尽可能小并且合适的J，那么这就需要用一个代码可编写的算法来寻找，这就是梯度下降算法。
我的理解就是，从J函数某个位置开始作为起点，根据导数去寻找J的最小值（导数为0），要注意的是，J函数可能有多个极小值点，所以不同的起点找到的值可能不同。
算法函数：

$$w = w - \alpha \frac{\partial}{\partial w} J(w, b)$$

$w$: 权重参数 (Weight)。左侧的 $w$ 是更新后的值，右侧是当前值。
$\alpha$ (Alpha): 学习率 (Learning rate)。它决定了我们沿着梯度方向“迈步”的大小。$\frac{\partial}{\partial w} J(w, b)$: 偏导数 (Derivative)。它代表了代价函数 $J$ 在当前 $w$ 点处的斜率，指明了函数值上升最快的方向。
同理对于其他权重，比如b也有：

$$w = w - \alpha \frac{\partial}{\partial b} J(w, b)$$

要注意的是在实际的梯度下降过程中，所有的权重是同步变化的，变化顺序就要准确获取，如下：

可见w和b是同步更新的，而不是一个更新再应用到另一个

学习率$\alpha$

可以理解为步长，即每次梯度下降的变化量大小。如果学习率比较大，那么值在进行梯度下降的时候一次走的值就会很大，可能会跳过一些合适的值；但是如果学习率很小，每次走的步长很小，寻找过程就会很慢。
所以我们应该寻找一个合适的学习率，或者让学习率能够采用自适应策略：因为越接近J的最小值，导数会越小，那么此时走的步长就应该小一些，此时可以让学习率根据导数的大小来变化。
利用上述公式进行计算：

$$\begin{aligned} \frac{\partial}{\partial w} J(w, b) &= \frac{\partial}{\partial w} \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \\ &= \frac{1}{2m} \sum_{i=1}^{m} \frac{\partial}{\partial w} (wx^{(i)} + b - y^{(i)})^2 \\ &= \frac{1}{2m} \sum_{i=1}^{m} 2(wx^{(i)} + b - y^{(i)}) \cdot x^{(i)} \\ &= \frac{1}{m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \end{aligned}$$

$$\begin{aligned} \frac{\partial}{\partial b} J(w, b) &= \frac{\partial}{\partial b} \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \\ &= \frac{1}{2m} \sum_{i=1}^{m} 2(wx^{(i)} + b - y^{(i)}) \cdot 1 \\ &= \frac{1}{m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)}) \end{aligned}$$

监督学习（Supervised learning 带有输入x和输出y）

• 回归算法（Regression Model）（常用于预测数据，输出有无数种可能）
• 分类算法(Classification Model)（顾名思义，用于分类，预测出的数据即为类别,少数可能的输出）

线性回归模型（Liner Regression Model）（监督学习中的回归算法）

输入只有一个维度，比方说房子的大小，输出也是一个维度，比方说房价。房价与房子大小之间的关系可以用一条线性函数来表示，通过两者关系的数据集可以拟合出一条合理的线性模型，这条线性模型就可以用来预测房价，即属于回归算法，

无监督学习（Unsupervised learning 只有输入x没有输出y，没有数据监督）

• 聚类算法（自己根据特征将其进行分类）
• 异常检测 （根据输入数据的特征寻找出异常的数据）
• 降维（将一个大的数据集压缩到小的数据集，但是尽可能多的保留信息）

多维

多维特征

实际的模型肯定不会像用房子大小预测房价一样，只有一个大小的特征。实际的模型肯定有很多特征feature（比如$x_1$:房子大小、$x_2$:浴室数量、$x_3$:楼层数量、$x_4$:已用年龄等等），一条这样的横向数据构成一个横向量。那么现在我们要有符号表示哪一个特征：$$x_j = j^{th}\text{feature}$$$$n = \text{number of feature}$$ $$\vec{x}^{(i)}=\text{features of }i^{th}\text{training example}$$$$x_j^{(i)}=\text{value of feature j in}i^{th}\text{training example}$$
可以理解为n为一条数据有几个输入作为特征。i表示第几条数据，j表示第几个特征。
最后这个多维线性模型：$$f_{w,b}(x)=w_1x_1+w_2x_2+...w_nx_n+b$$$$\vec{w}=[w_1,w_2,...w_n]$$$$\vec{x}={x_1,x_2,...x_n }$$$$f_{\vec{w},b}=\vec{w}\cdot{}\vec{x}+b$$

向量化

或者叫矢量化，能让代码更简洁，运行起来更快（有GPU）。
example：$$\vec{w}=[w_1\ w_2\ w_3]$$$$b\ \text{is a number}$$$$\vec{x}=[x_1\ x_2\ x_3]$$
在python代码中可以用一个线性代数库NumPy来将列表转化为numpy的array（向量对象）

import numpy as np
w = np.array([1.0, 2.5, -3.3])
b = 4
x = np.array([10, 20, 30])
#我们要计算点积可能会想到用一个循环来求和，如下：
# f = 0
# for j in range(n):
#   f = f + w[j] * x[j]
# f = f + b
#但是并不够简洁，numpy给我们提供了更简洁的函数
f = np.dot(w,x) + b

使用向量化进行计算实际上是更快的，因为循环是一个串行的操作，但是dot函数会并行计算点积，最后将点积相加。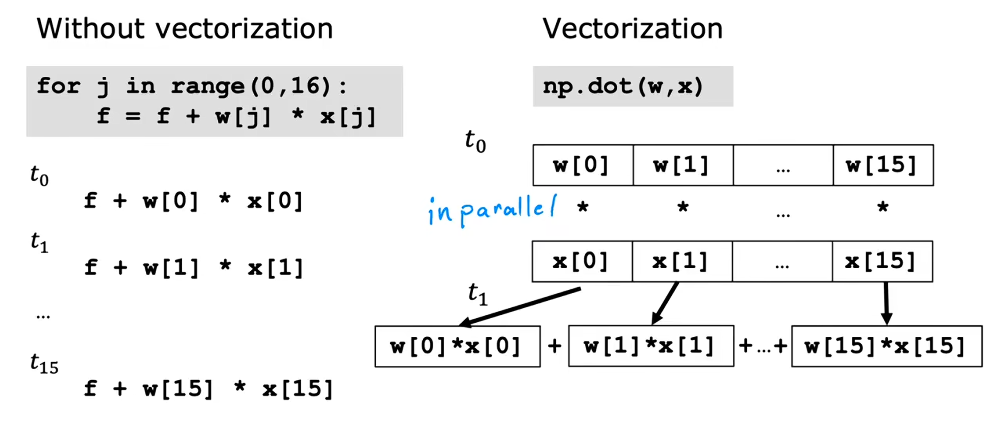

所以向量化后，很多计算都是并行处理的，会快很多。

多元线性回归的梯度下降

在多元场景下，每个参数 $w_j$ 的更新都需要用到对应的特征分量 $x_j^{(i)}$。
权重 $w_j$ 的更新

$$w_j = w_j - \alpha \frac{1}{m} \sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right) x_j^{(i)}$$

偏置 $b$ 的更新

$$b = b - \alpha \frac{1}{m} \sum_{i=1}^{m} \left( f_{\vec{w},b}(\vec{x}^{(i)}) - y^{(i)} \right)$$

特征放缩

能够让梯度下降运行更快的一种算法。
简单来说，特征放缩就是为了把形状怪异的“深谷”变成圆润的“碗”：如果特征范围差距过大（如面积 2000 对比卧室数 2），损失函数的等高线会变得极其扁长，导致梯度下降在寻找最优解时反复震荡、走弯路；通过放缩让各特征处于同一数量级，能让算法走直线、不跑偏，从而极大地加快模型收敛的速度。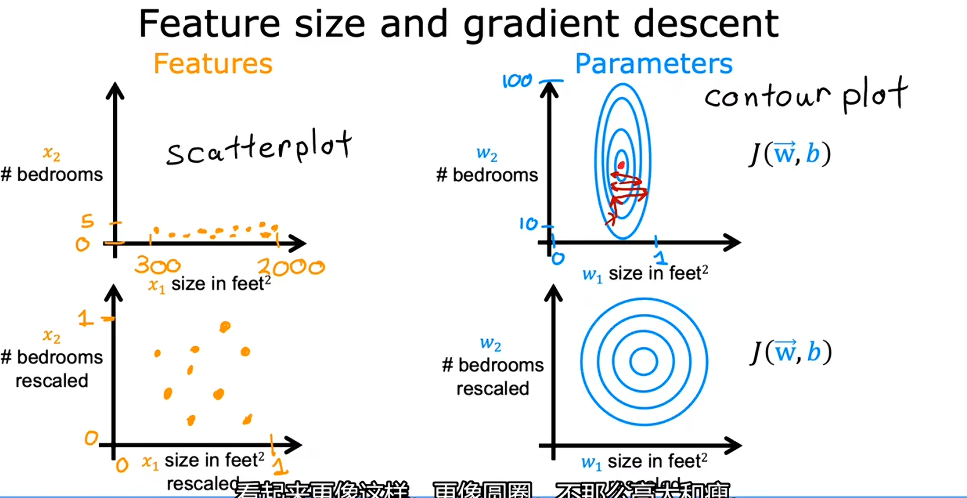

特征放缩算法

• Feature scaling：将特征范围都除以最大值，这样特征范围最大值就会被限制在1。
  
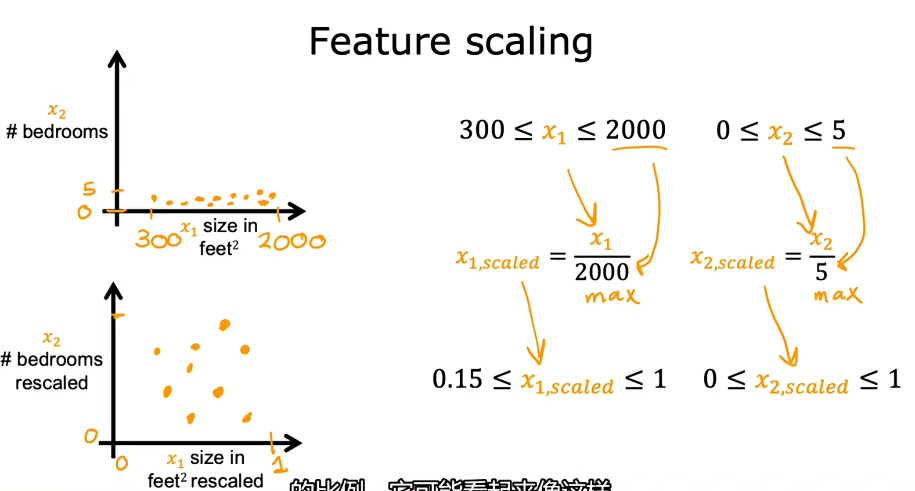
• Mean normalization（均值归一化）：取特征的平均值$u_j$,对于每个特征值都如此计算$\frac{x_j-u_j}{x_{max}-x_{min}}$ 这样的话特征范围就被限制在-1到1
  
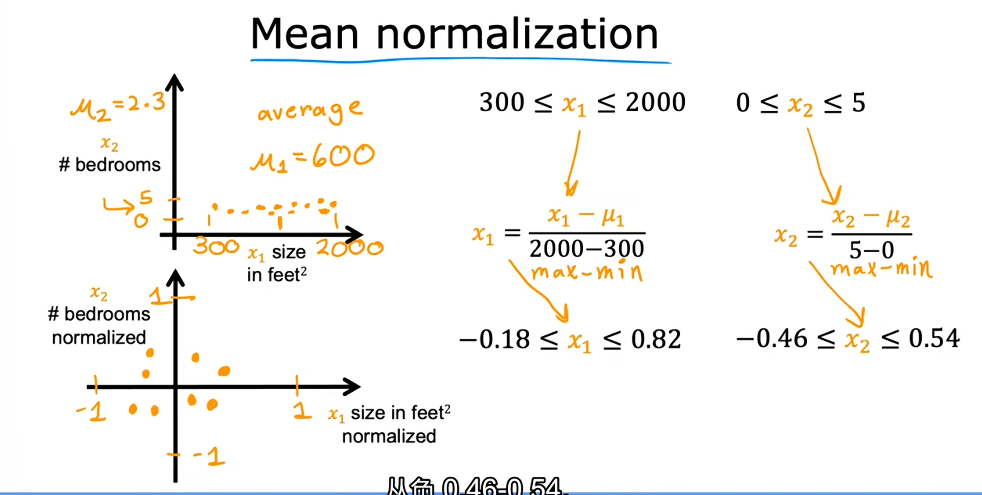
• Z-Score normalization:计算每个特征的标准差$\sigma_{j}$,对于每个特征值都计算$\frac{x_j-u_j}{\sigma_j}$.
  

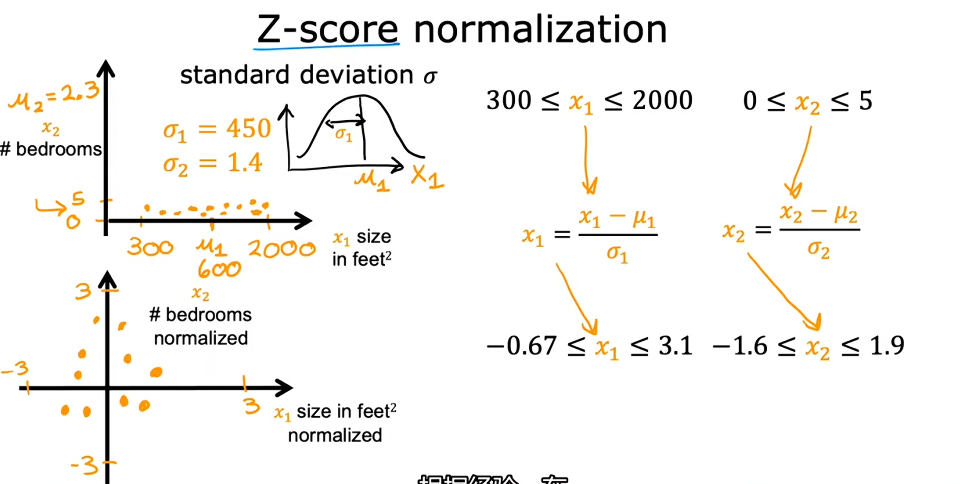
放缩后各个特征范围尽量相仿并且合理较小，如果某个特征范围相对较大或者过小可以继续对其进行放缩。

判断梯度下降是否收敛（converging）

以代价函数值$J(\vec{w},b)$为纵坐标，以梯度下降迭代次数为横坐标的函数曲线图称为学习曲线，一般来说J要随着迭代次数逐渐减小。如果这个曲线随着迭代次数有增加，说明学习率$\alpha$不合适（过大）或者代码出现错误。
经过多次迭代之后，这个学习曲线就会收敛到一个较小的值，但是我们一开始并不知道迭代次数，所以要确定模型何时收敛一种方法是建立所说的学习曲线，另一种则是使用自动收敛测试（Automatic convergence test）。
自动收敛测试:让$\epsilon$代表一个较小值，比如0.001，如果一次迭代之后J的减小值比这个$\epsilon$还要小，你就可以确定收敛了，但是要找到一个合适的$\epsilon$是比较困难的，所以更多情况下可以用学习曲线.

如何设置一个比较好的学习率$\alpha$

之前我们学到了，学习率太大会导致学习曲线不能收敛，在谷间波荡，太小又会导致收敛速度过慢。当学习曲线一直是增加的时候，有可能是学习率设置太大了，也有可能是代码出错了（把-写成了+），这个时候可以设一个较小的学习率来测试一下，如果还是一直增加，大概率就是代码问题。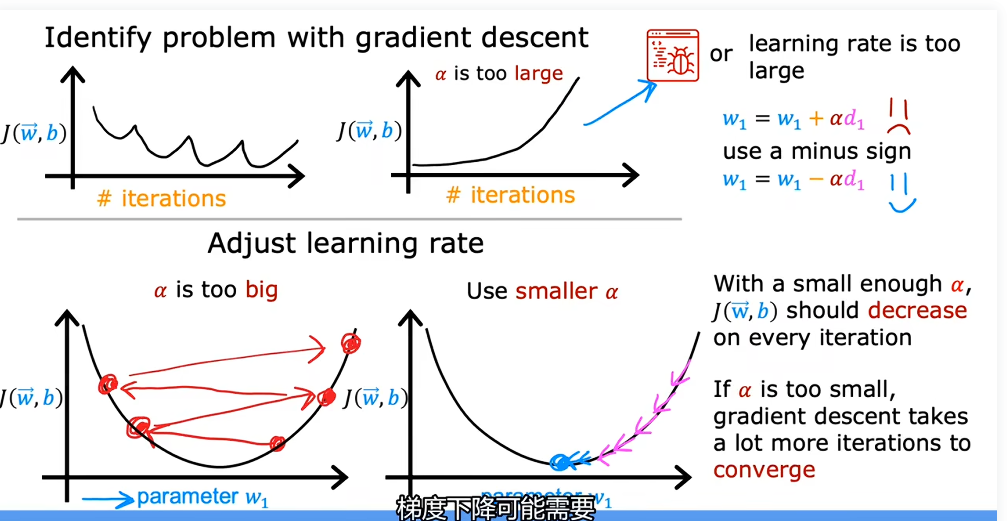

实际训练过程中可能会选择多个学习率的值，从较小的开始尝试，每次放大几倍，找到比较合适的学习率。

特征工程（Feature Engineering）

还是以预测房价举例，一个房子的房价可能跟它的长和宽有关系，但是实际上更跟面积即长乘宽有关系，这个时候特征就变成了一个。
新建一个特征就是特征工程的一个例子，能够让算法更简单。

多项式回归

用来拟合非线性的方程，不同的数据，应当选择合适的多项式函数来进行拟合，$x^n$？$\sqrt{x}$？

逻辑回归算法（logistic regression）

虽然叫逻辑回归但是实际上不算是回归模型，跟之前我们学到的一样，回归模型一般是用来预测数据的，范围比较大，这个命名是历史原因，不用管。
线性回归并不是一个解决分类问题的好算法，他表示的是一个大范围的数值，而分类是几个可能的数值，这就需要我们引入逻辑回归。
比较简单的分类只有两种情况，true和false，在计算机中用1和0表示，也可以称为positive clas和negative class（不是语义上的）。
实际训练过程中，模型也可能是一个线性的，输出数据可能千奇百怪，这个时候我们需要设置一个阈值，比如0.5，让小于0.5置为0，大于0.5置为1.此时我们需要引入sigmoid函数或者称为logistic函数：$$\frac{1}{1+e^{{-x}}$$.$$z=\vec{w}\cdot\vec{x}+b$$$$g(z)=\frac{1}{1+e}{-z}}$$

$$f_{\vec{w},b}=g(\vec{w}\cdot\vec{x}+b) = \frac{1}{1+e^{-(\vec{w}\cdot\vec{x}+b)}}$$

这就是逻辑回归的精髓： 先用线性模型计算出一个“得分” $z$，再用 Sigmoid 函数把这个得分“压”进 0 到 1 的概率区间里。$g(z)$ 的作用：压制范围（映射）。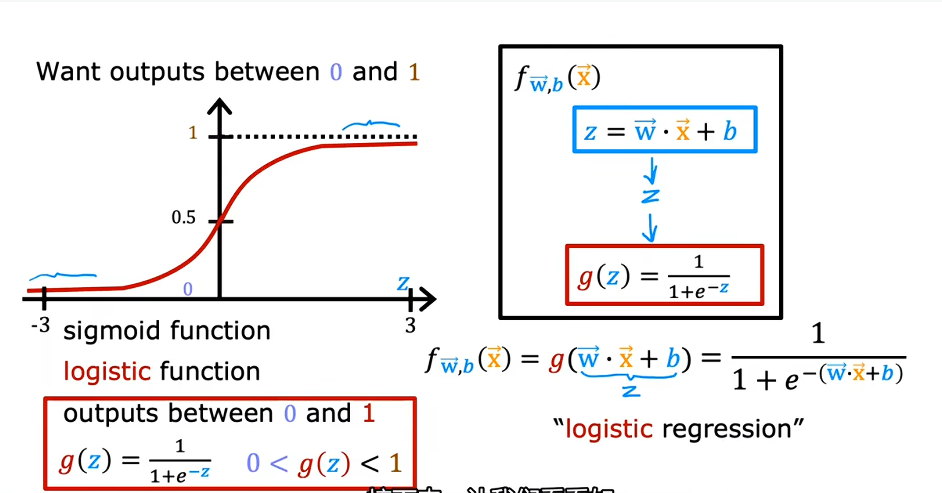

决策边界（Decision boundary）

我们sigmoid函数将数值映射为分类概率，那么我们就要知道映射概率的边界，什么范围的映射概率到哪个分类。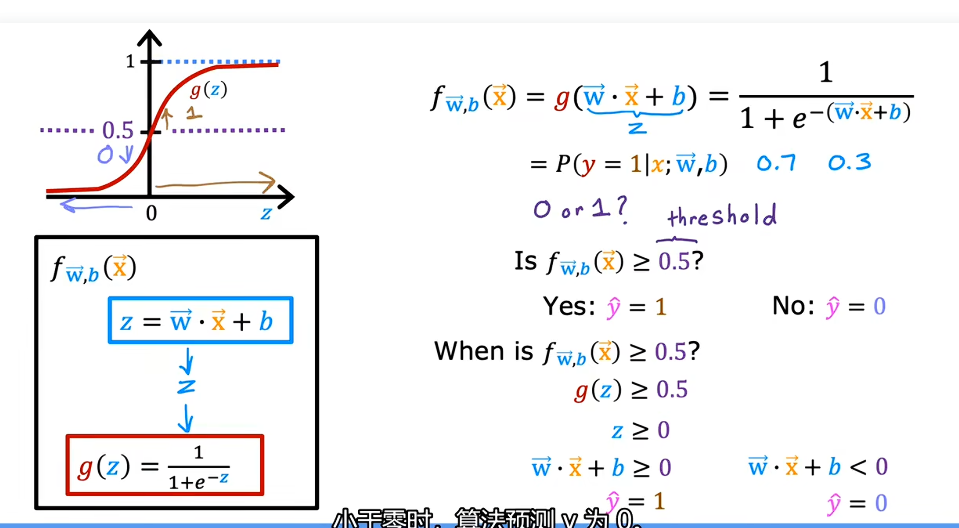

一般来说g(z) = 0.5为边界，当g(z)大于等于0.5时，分类为1，g(z)小于0.5时分类为0.再根据$z = \vec{w}\cdot\vec{x}+b$,z >= 0时分类为1，z < 0时，分类为0.
决策边界是画在你的原始数据图（比如 $x_1$ 为横轴，$x_2$ 为纵轴的图）里的。它是用来告诉你在特征空间里，哪块地盘属于 A，哪块地盘属于 B。比如：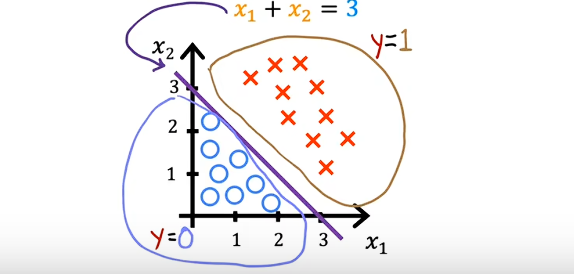


实际的决策边界可能是各种形状。

逻辑回归模型中的代价函数

在线性回归模型中，代价函数是一个凹陷的函数只有一个极小值，公式是使用平方差求和$J_{\vec{w},b} = \frac{1}{2m}\sum_{i=1}^{m}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})^2$但是对于逻辑回归模型若用相同的方法进行求成本函数，你会发现逻辑回归的成本函数变成了一个多极小值的凹凸不平的函数，并不合要求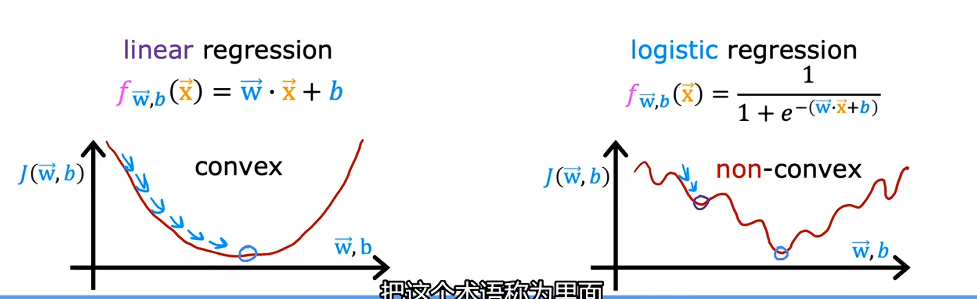

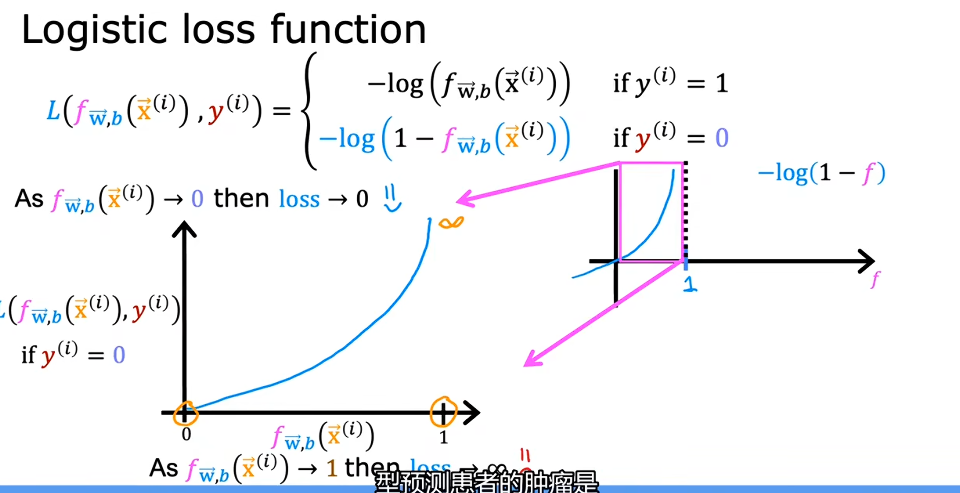
所以我们要用一个新的成本函数：the loss on a single training example$L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})$,我们称其为损失函数。

$$L(f_{\vec{w},b}(\vec{x}^{(i)}), y^{(i)}) = \begin{cases} -\log(f_{\vec{w},b}(\vec{x}^{(i)})) & \text{if } y^{(i)} = 1 \\ -\log(1 - f_{\vec{w},b}(\vec{x}^{(i)})) & \text{if } y^{(i)} = 0 \end{cases}$$

$$J(\vec{w},b)=\frac{1}{m}\sum_{i=1}^{m}L(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})$$

我们可以来看看L的两个分叉

因为sigmoid函数概率只能取到0-1，所以定义域也就确定了，当实际值y为1的时候，如果我们预测的$\hat{y}$也是1，那么根据L，此时代价是0，没有惩罚，但是如果我们的预测值$\hat{y}$是0，那么根据L，代价就是无穷大，惩罚严重。
同理，当实际值为0时，对对数函数进行变化，如下：

简化逻辑回归